¶写在前面
说起来,当初MIT 18.06这个课程完全是网络投喂给我的,知乎、B站上好多同学对他交口称赞,抱着看着玩的态度看了第一集,立刻被 Strang 老师的幽默,课程的严谨,有趣的授课方式所折服,就一直看了下去。
谁也想不到这个讲线性代数的课会涉及到 正规方程 的推导,我也更没想到,周二看完的 特征值与特征向量的应用后,周三的机器学习马上讲了PageRank算法,而算法一种独特的求解方法,恰巧使用了特征值与特征向量的性质。
这种知识点的交错简直太棒了。
所以这篇文章讲首先回顾特征值、特征向量是什么,怎么算,再说一说由此带来的优美的性质,最后用两个应用实例 斐波那契数列的求解、PageRank的幂解法(power method)结束。
¶特征值、特征向量
网络上有很多特征值、特征向量的介绍,所以我在这里还是简单粗暴的用一个例子来过一下它们是啥、怎么求、有什么性质。
¶举例
有一个矩阵A,它长这样子A=[3 1;1 3]:
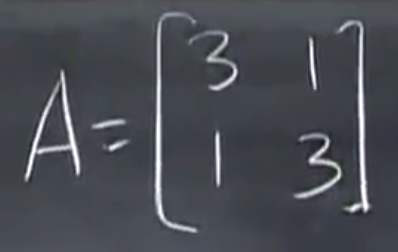
我们想求这个矩阵的特征值、特征向量,我们怎么做?
构造 $A-\lambda I$ 矩阵,这个矩阵的行列式值为零,即可求出特征值,以下为求解步骤:
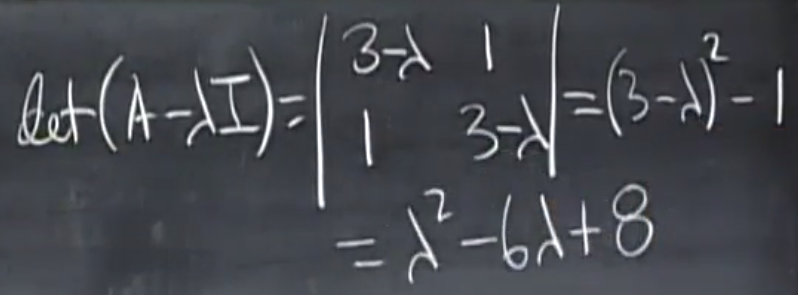
这样我们就求出来,两个特征值分别为 2 和 4 ,那特征向量呢?
特征向量就是矩阵 $A-\lambda I$ 的零空间,也就是方程 $(A-\lambda I)x=0$ 的解 $x$ ,这也很好求,代入即可。
对特征值 4 ,它的特征向量是 $x_1 = [1;1]$ ,对于特征值 2 ,它的特征向量是 $x_2 = [-1; 1]$。
¶意义
所以,我们费劲巴列的算出这两个东西是干啥用呢?这要从两个方面说起,从定义上讲。特征向量是与原矩阵相乘之后方向不改变的向量,有些费解?还是用例子解释:
我们刚才的A矩阵,与第一个特征向量相乘,$Ax_1=x_{new}=[4;4]$ ,发现没有,这个新得到的向量 $x_{new}$ ,它和原先向量 $x_1 = [1;1]$ 方向完全一致,同时$x_{new} = 4×x_1$,这个倍数4,就是我们对应的特征值 $\lambda$ ,于是我们就得到了非常重要的公式:
$$
Ax=\lambda x
$$
稍微处理一下:
$$
Ax-\lambda x=0
$$
$$
(A-\lambda I)x=0
$$
所以,要得到非零向量x,矩阵$A-\lambda I$ 必须是奇异的,也就是它的行列式必须为零(这也解释了为什么刚刚我们的方法可以求出特征值$\lambda$)
而计算特征向量的第二个原因,就是它代表了矩阵很多的特征(废话),具备很多优美的性质,可以应用在很多地方,下面所述的两个例子,就是其在求幂 这个过程中起到了非常大的作用。
优美的性质,激动人心的案例,马上就来。
¶优美的性质
¶对角化
为了避免这篇文章变得又臭又长,对这个不是很美丽的性质,我们就把它拿出来看一看,不做过多介绍。
¶白话版描述
如果你给我一个n维方阵,就比如说A,如果这个矩阵不那么特殊,也就是它能求得n个互不相关的特征向量,也就是这n个向量可以支撑起整个n维空间,那么我通过下面这个式子,可以把你给我的A变成一个对角方阵,而且对角线上就是n个特征值。
$$
S^{-1}AS=\Lambda
$$
这里的S,就是特征值组合成的方阵,我还是拿刚才的A举例子,对A来说,S是这样的

那我们就看看,最后乘出来是啥吧:

哈哈,是不是,既是一个对角方阵,而且对角线上的值还是特征值,有意思吧,其实推的话也很好推,只是篇幅限制,感兴趣的同学可以去听18.06特征向量这一节。
这里我们就记住下面这个公式就好啦:
$$
S^{-1}AS=\Lambda
$$
¶求幂
对上面的公式稍微做些变化:
$$
A = S\Lambda S^{-1}
$$
$$
A^2 = S\Lambda S^{-1}S\Lambda S{-1}=S\Lambda{2}S^{-1}
$$
可以看到,求幂后,特征向量组成的S方阵并没有变化,只是特征值也做了幂操作,事实上,如果我们看特征向量的定义式:
$$
Ax=\lambda x
$$
$$
A^2x=\lambda Ax=\lambda ^2x
$$
也可以看出,特征向量没变,特征值与A同时加幂。这样的性质,就为我们求幂,提供了新的思路。
考虑一个递归式子(给定u0和A),求uk:
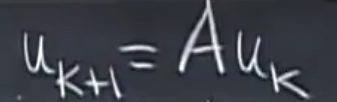
如果编程实现的话,非常方便,但是这样的操作涉及到k次的矩阵乘法,而且无法并行,非常耗时,有什么办法可以直接一步求解吗?
当然可以,特征向量闪亮登场!
写出式子的前几项:
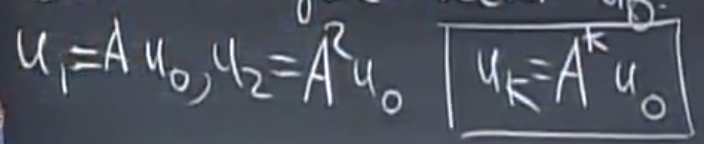
这个时候,我们可以把每个u,都写成n个特征向量线性组合的形式(因为这些特征向量是线性无关的,可以撑起整个n维空间,所以任何向量都可以表示成这样的线性组合)。
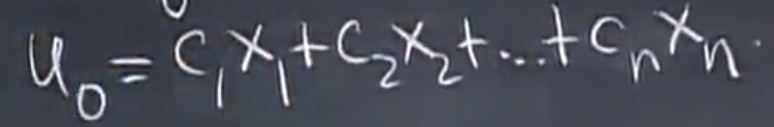
这里
$$
u_0 = c_1x_1 +c_2x_2+…+c_nx_n = Sc
$$
两边同时乘上A,可以得到:
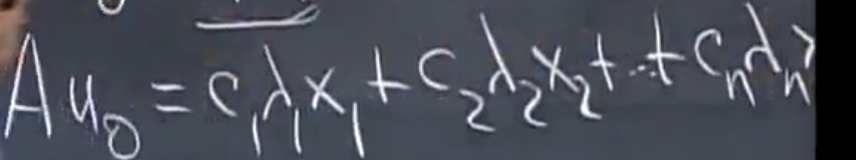
这个时候,如果我们把A求100幂,结果会怎样呢?
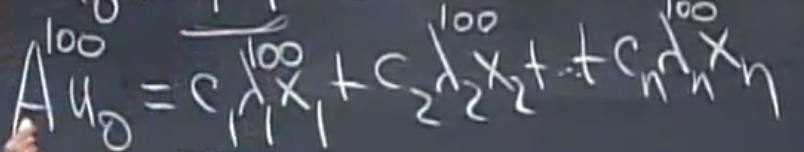
再向下推一步就可以得到
$$
A^{100}u_0 = S\Lambda ^{100}c
$$
还记得S和c是啥吧,就是n个特征向量组合起来的方阵和得到u0的线性组合参数。
到这里,问题就迎刃而解啦
$$
u_k = A^ku_0=S\Lambda ^kc
$$
通过这个式子就可以一步求出解啦。
¶应用
¶斐波那契数列
斐波那契数列是一个很经典的递归求解的案例,我们看看特征向量是怎么派上用场的吧~
首先,给出问题形式:
$$
F(n+2)=F(n+1) + F(n) ,给定F(0)=0,F(1)=1
$$
手算的话,前几项是这样的
0 1 1 2 3 5 8 13 21 34 55 89 144 233
问题来了,怎么通过一次,而不是递归的得到问题的解呢?
相信打过ACM比赛的人都知道 二分之跟号五+1,但是这个数咋来的呢?一起来看
¶问题转换
这里是膜拜Strang老师的有一个地方,通过一个非常巧妙的trick,把二阶问题转化为了一阶:
令uk为下面这个:
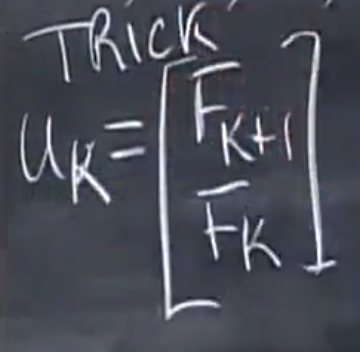
那么,$u_{k+1}$ 就可以用这个矩阵得到:
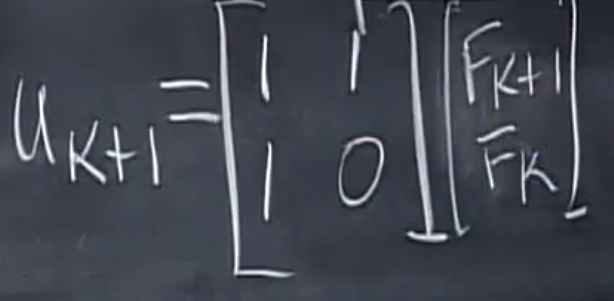
问题转化为我们熟悉的形式,同时这个A也得到了。
下一步就是,计算特征值、特征向量,S,c,相乘,得到结果,这个过程,我用下面这段代码描述:
1 | lambda1 = 1.6180 |
最后得到,result = 1.0e+20 * 3.5348 而通过递归算法求得的真实值是3.5422e+20,太美妙了有没有?
¶PageRank算法的幂解
哈哈标题写那么大,写道这里才涉及到PageRank,好惭愧。
更惭愧的是,这里不打算对PageRank做基本的介绍,因为李航老师的书里写的实在太过于清晰了,事实上,关于,幂解,我也仅仅打算从李老师那里copy过来,目的就是让大家感受下,这个方法,几乎原封不动,就是我们刚刚说到的那个求幂的方法:



我预感这两个图片很可能会挂,所以如果有同学想看手头没有书的话,可以联系邮箱tjcxs136720@163.com我发给你~