leetcode-week1

¶第一题

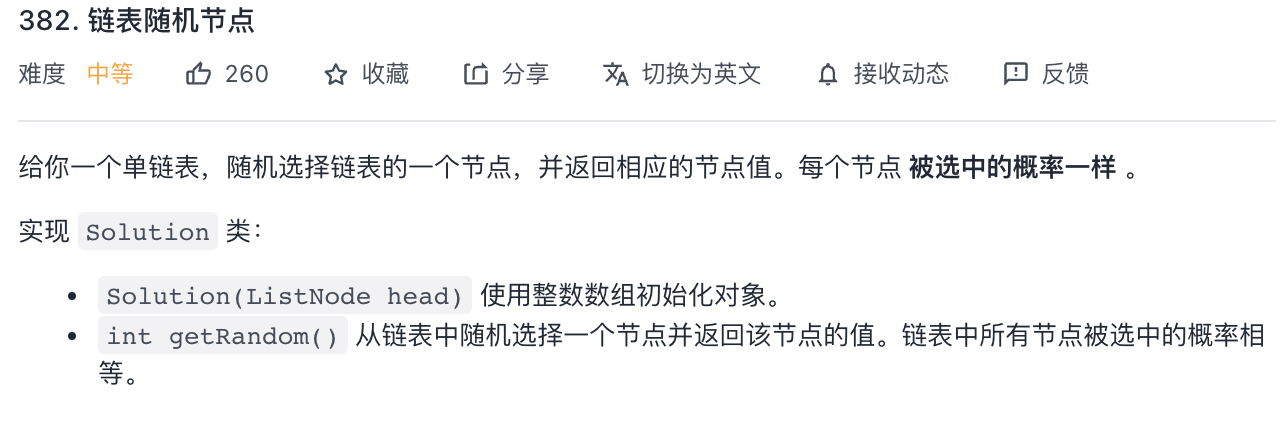
这个挺简单的，就是用一个数组记录所有内容，然后随机就完事了：

class Solution {
public:
    vector<int> list;
    Solution(ListNode* head) {
        while(head){
            list.push_back(head->val);
            head = head->next;
        }
    }
    int getRandom() {
        return list[rand() % list.size()];
    }
};

但这并不是我们想要的，这道题原始是希望不知道数据总体有多大时，也能做到随机取样（不能加载所有数据时）

¶蓄水池抽样算法

即：当内存无法加载全部数据时，如何从包含未知大小的数据流中随机选取k个数据，并且要保证每个数据被抽取到的概率相等。

当 k = 1 时，即此题的情况
也就是说，我们每次只能读一个数据。

假设数据流含有N个数，我们知道如果要保证所有的数被抽到的概率相等，那么每个数抽到的概率应该为 1/N

那如何保证呢？

先说方案：

每次只保留一个数，当遇到第 i 个数时，以 1/i的概率保留它，(i-1)/i的概率保留原来的数。

举例说明： 1 - 10

遇到1，概率为1，保留第一个数。
遇到2，概率为1/2，这个时候，1和2各1/2的概率被保留
遇到3，3被保留的概率为1/3，(之前剩下的数假设1被保留)，2/3的概率 1 被保留，(此时1被保留的总概率为 2/3 * 1/2 = 1/3)
遇到4，4被保留的概率为1/4，(之前剩下的数假设1被保留)，3/4的概率 1 被保留，(此时1被保留的总概率为 3/4 * 2/3 * 1/2 = 1/4)
以此类推，每个数被保留的概率都是1/N。

代码为：

class Solution {
public:
    Solution(ListNode* head) {
        this->head = head;
    }
    
    /** Returns a random node's value. */
    int getRandom() {
        ListNode* phead = this->head;
        int val = phead->val;
        int count = 1;
        while (phead){
            if (rand() % count++ == 0)
                val = phead->val;
            phead = phead->next;
        }
        return val;
    }
    ListNode* head;
};

¶第二题 1220

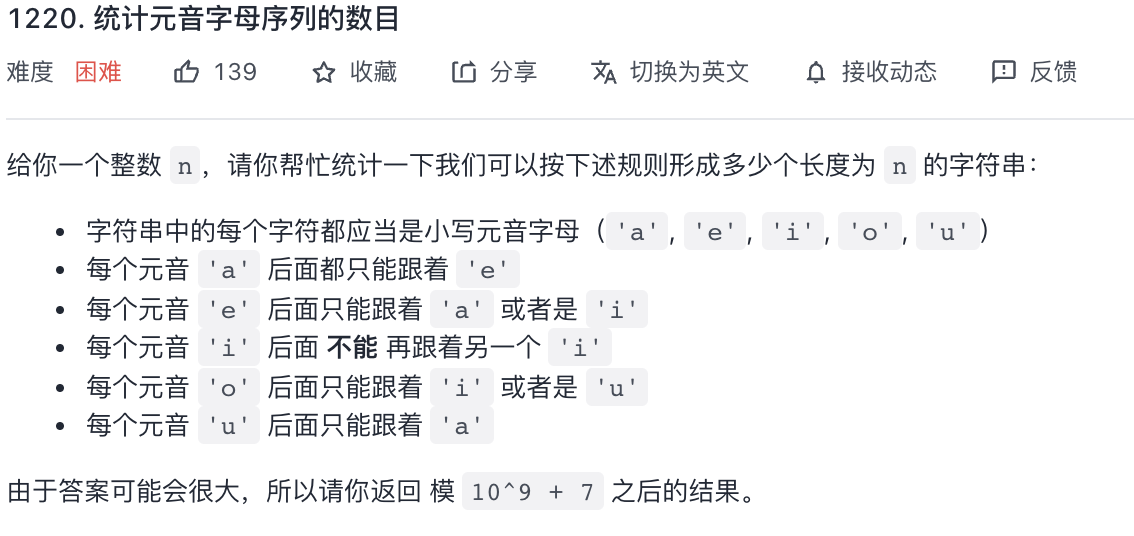
这里就是个dp或者用矩阵快速幂
dp

class Solution {
public:
    int countVowelPermutation(int n) {
        long long mod = 1e9 + 7;
        vector<long long> dp(5, 1);
        vector<long long> ndp(5);
        for (int i = 2; i <= n; ++i) {
            /* a前面可以为e,u,i */
            ndp[0] = (dp[1] + dp[2] + dp[4]) % mod;
            /* e前面可以为a,i */
            ndp[1] = (dp[0] + dp[2]) % mod;
            /* i前面可以为e,o */
            ndp[2] = (dp[1] + dp[3]) % mod;
            /* o前面可以为i */
            ndp[3] = dp[2];
            /* u前面可以为i,o */
            ndp[4] = (dp[2] + dp[3]) % mod;
            dp = ndp;
        }
        return accumulate(dp.begin(), dp.end(), 0LL) % mod;
    }
};

快速幂
待查，以后再补这一点吧

¶第三题 539

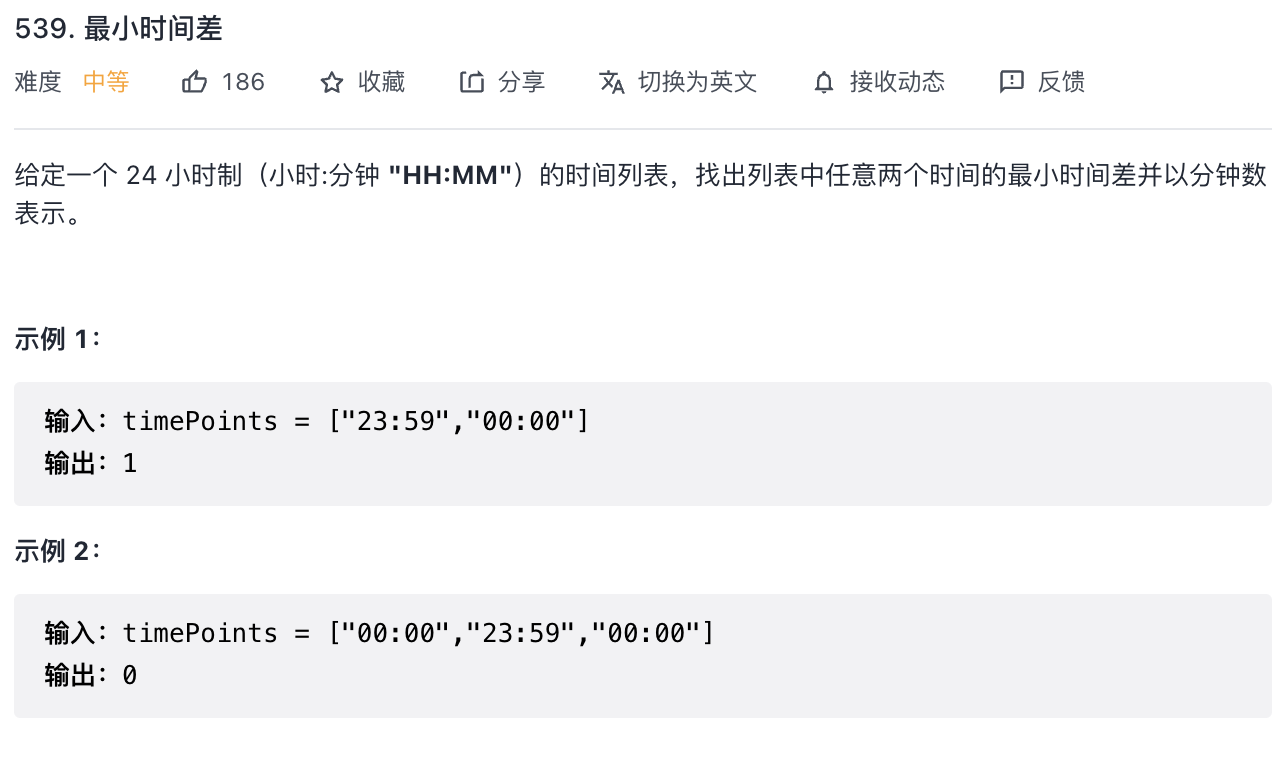
先排序，然后转换为分钟，再遍历：

class Solution {
    int getMinutes(string &t) {
        return (int(t[0] - '0') * 10 + int(t[1] - '0')) * 60 + int(t[3] - '0') * 10 + int(t[4] - '0');
    }

public:
    int findMinDifference(vector<string> &timePoints) {
        sort(timePoints.begin(), timePoints.end());
        int ans = INT_MAX;
        int t0Minutes = getMinutes(timePoints[0]);
        int preMinutes = t0Minutes;
        for (int i = 1; i < timePoints.size(); ++i) {
            int minutes = getMinutes(timePoints[i]);
            ans = min(ans, minutes - preMinutes); // 相邻时间的时间差
            preMinutes = minutes;
        }
        ans = min(ans, t0Minutes + 1440 - preMinutes); // 首尾时间的时间差
        return ans;
    }
};

¶第四题 219

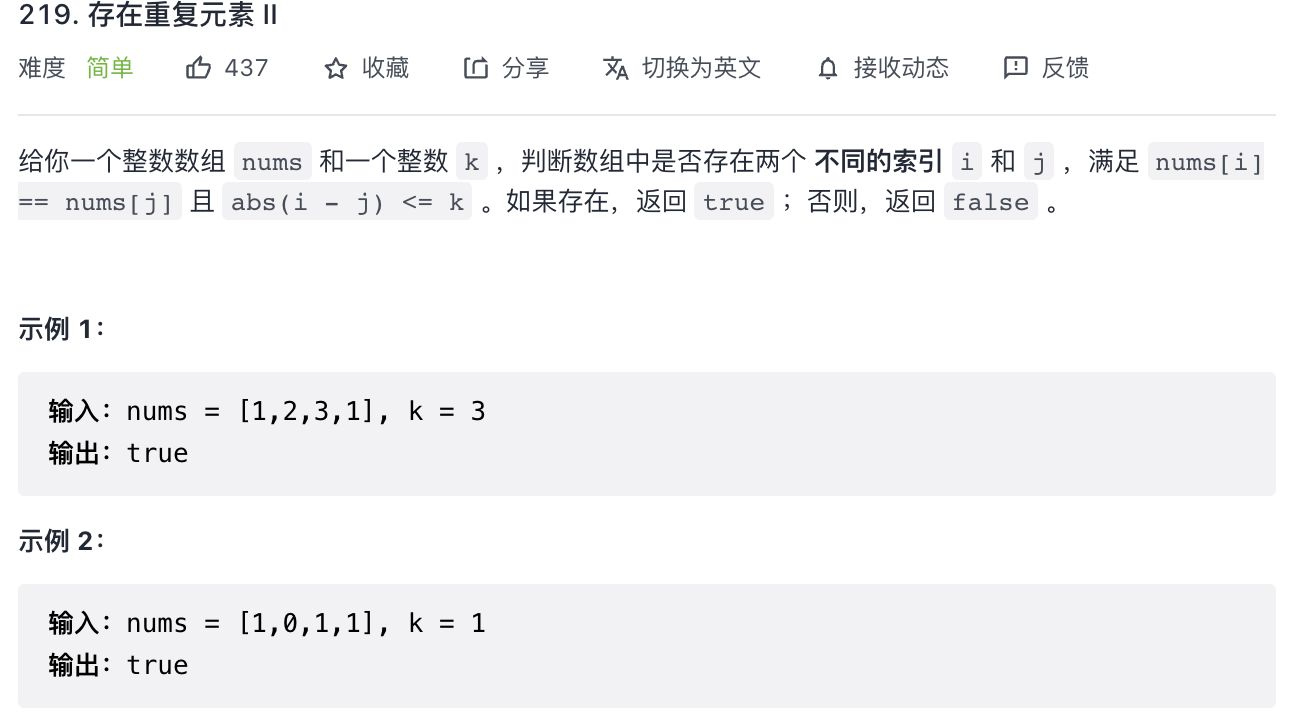
hashmap 的巧妙利用

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        unordered_map<int, int>myMap;
        for (int i = 0; i < nums.size(); i++) {
            if (myMap.count(nums[i]) && i - myMap[nums[i]] <= k) {
                return true;
            }
            myMap[nums[i]] = i;
        }
        return false;
    }
};

¶第五题 2029

这题并不知道怎么做，抄的，待查

class Solution {
public:
    bool stoneGameIX(vector<int>& stones) {
        int s[3] = {0, 0, 0};
        for (int i : stones) ++s[i % 3];
        if (s[0] % 2 == 0) return s[1] != 0 && s[2] != 0;
        return s[2] > s[1] + 2 || s[1] > s[2] + 2;
    }
};

¶第六题 1345

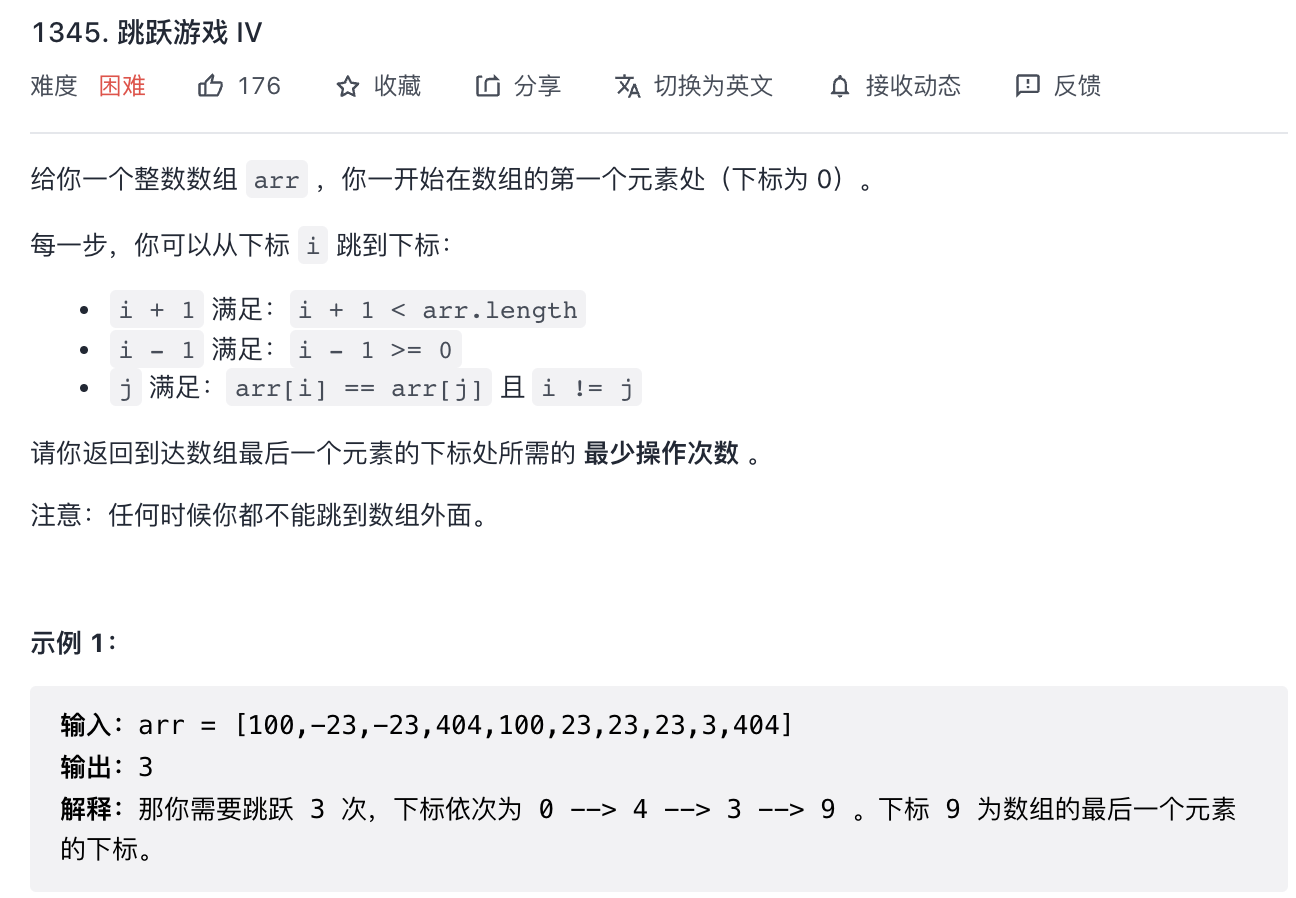
这题也待查吧，先放在这里：

class Solution {
public:
    int minJumps(vector<int>& arr) {
        const int inf = 0x3f3f3f3f;
        int n = arr.size();
        unordered_map<int, vector<int>> map;
        for(int i = n - 1; ~i; i--) {
            map[arr[i]].push_back(i);
        }
        vector<int> dist(n, inf);
        queue<int> q;
        q.push(0);
        dist[0] = 0;
        while(q.size()) {
            auto t = q.front(), step = dist[t];
            q.pop();
            if(t == n - 1) return step;
            if(t + 1 < n and dist[t + 1] == inf) {
                q.push(t + 1);
                dist[t + 1] = step + 1;
            }
            if(t - 1 >= 0 and dist[t - 1] == inf) {
                q.push(t - 1);
                dist[t - 1] = step + 1;
            }
            const auto& list = map[arr[t]];
            for(auto ne :list) {
                if(dist[ne] == inf) {
                    q.push(ne);
                    dist[ne] = step + 1;
                }
            }
            map[arr[t]].clear(); //or map.erase(arr[t]);
        }
        return -1;
    }
};

¶第七题

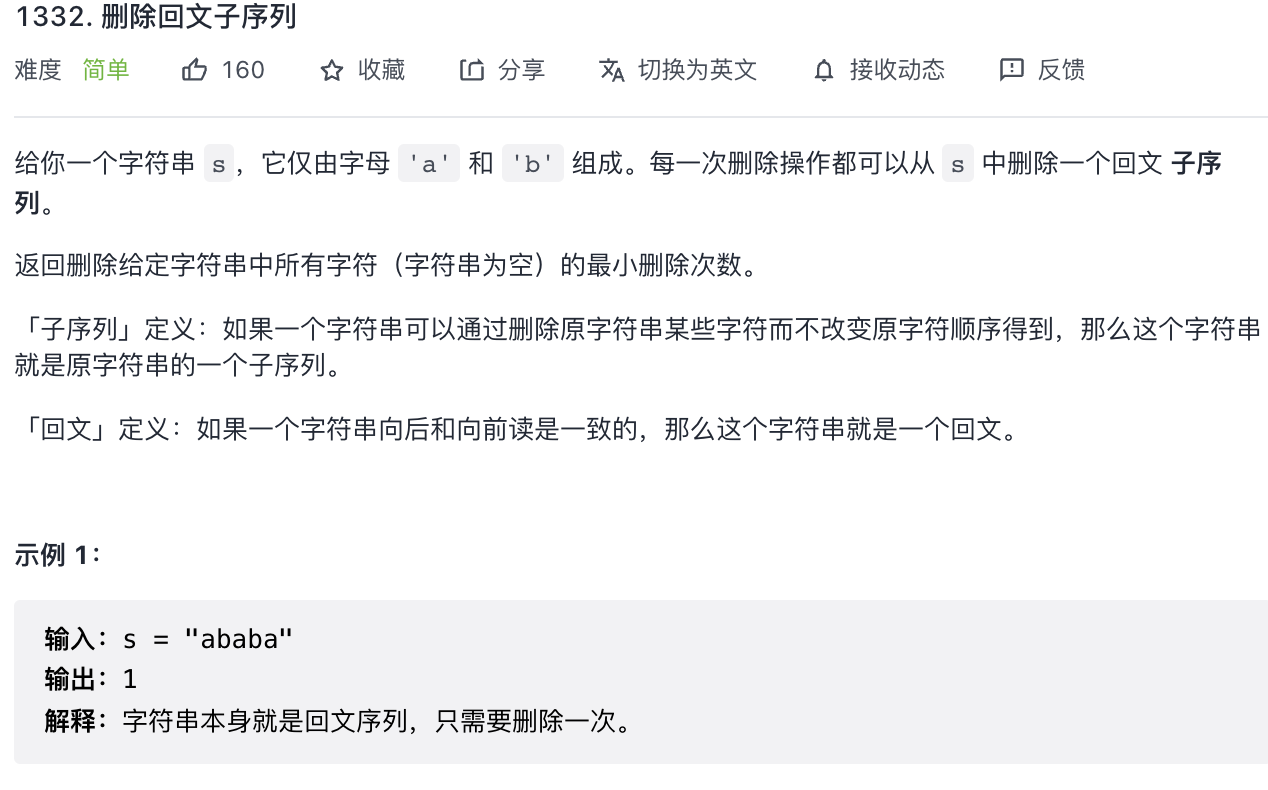
这个太简单了，就判断一下是不是回文，如果是，一步就够了，如果不是，也就两步。

class Solution {
public:
    int removePalindromeSub(string s) {
        int n = s.size();
        for (int i = 0; i < n / 2; ++i) {
            if (s[i] != s[n - 1 - i]) {
                return 2;
            }
        }
        return 1;
    }
};