¶写在前面
这篇文章写给已经对SVM有所了解,但是对背后的公式和方法还有所迷惑的同学,有些图片和思路借鉴于下面三篇博客:
https://www.jiqizhixin.com/articles/2018-10-17-20
https://blog.csdn.net/weixin_41500849/article/details/80493712
https://www.cnblogs.com/liaohuiqiang/p/7805954.html
另外,由于本人能力有限,且没有严谨的数学功底,同时又极力想把这个问题描述得非常简单,所以文中肯定会有不合理乃至错误之处,还请大家不吝指正。
¶拉格朗日乘子法
接触过 SVM 的同学应该都听过这个方法,不过我一开始听到这个方法时是完全懵逼的,再加上KKT条件,整个人傻掉了,下面,咱就用一个最简单的例子,说一说这个拉格朗日乘子法,是个啥意思。
¶问题描述
首先,我们把问题限制在凸函数的优化问题上,也就是没有多个 local minimal,只有一个全局最优。
最简单的问题就是:下面这个函数的最小值是多少?
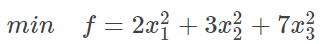
那位读者你把手放下,我知道你学过,不就是求导吗?当我没上过高中啊?好吧好吧,那如果加上一个条件呢?
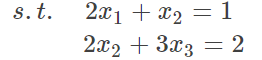
如果不但要保证$f$ 最小,同时还要满足上面两个等式,该咋整捏?我们一点点来看。
¶等式约束
没错,咱们上面描述的那个问题就是一个带等式约束的优化问题,但是三个$x$太多了,咱们看一个简单的:
目标函数:
$$
f(x_1, x_2) = x_1 + x_2
$$
等式约束:
$$
h(x) = x_12+x_22-2=0
$$
画出来是什么样子呢?

f(x)在二维平面上画出等高线(contour)就是一条条斜率相同的直线,h(x)=0在二维平面上画出等高线就是一个圆,如上图所示。
可以明显的看出,在圆圈h(x)的限制下,直线 $f(x)$ 的最小值为-2,在左下角直线x1+x2=2和圆的交点上。
不考虑圆h(x)的限制时,f(x)要得到极小值,需要往f(x)的负梯度(下降最快的方向)(不懂为什么负梯度是下降方向的同学可以用个最简单的二次方程试一试,确实是这样的)方向走,如下左图蓝色箭头。
如果考虑圆h(x)的限制,要得到极小值,需要沿着圆的切线方向走,如下右图红色粗箭头。注意这里的方向不是h(x)的梯度,而是正交于h(x)的梯度,h(x)梯度如下右图的红色细箭头。
在极小值点,f(x)和h(x)的等高线是相切的。
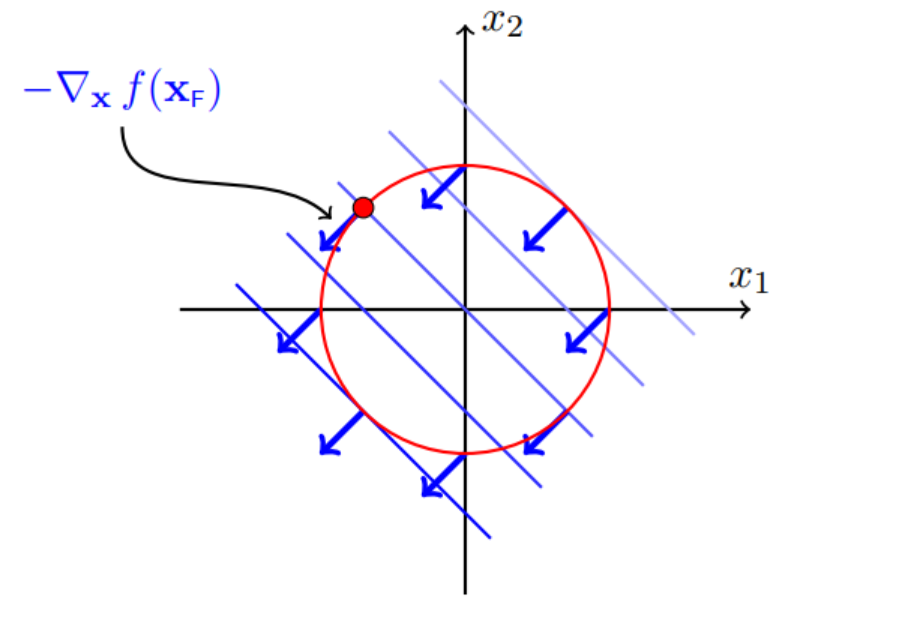
容易发现,在关键的极小值点处,f(x)的负梯度和h(x)的梯度在同一直线上,如下图左下方critical point的蓝色和红色箭头所示。

由此可知,在极小值点,h(x)和f(x)的梯度在同一线上,有
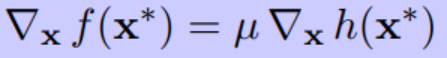
所以,对于f(x)和h(x)而言,只要满足上面这个式子,同时使得h(x) = 0,解得的x就是我们要求的极小值点(或极大值点,为了简单起见我们只讨论极小值点)
要做到这一点,可以构造一个拉格朗日函数,对函数令偏导等于0求解,恰好等价于“满足上面这个式子,同时使得h(x) = 0",原问题转化为对拉格朗日函数求极值问题,这就是拉格朗日乘子法。

¶不等式优化
上面我们说的是等式,那对于不等式又该如何应对呢?
不等式优化涉及到两种情况,我们分别来看:
¶极小值点落在可行域内(不包含边界)
考虑目标函数$f(x)=x_12+x_22$,不等值约束$g(x)=x_12+x_22−1$,显然f(x)的极小值为原点(0,0),落在可行域内。可行域以原点为圆心,半径为1。
这种情况约束不起作用,考虑极小值点x*,这个时候,g(x*) < 0,f(x*)的梯度等于0。
¶极小值点落在可行域外(包含边界)
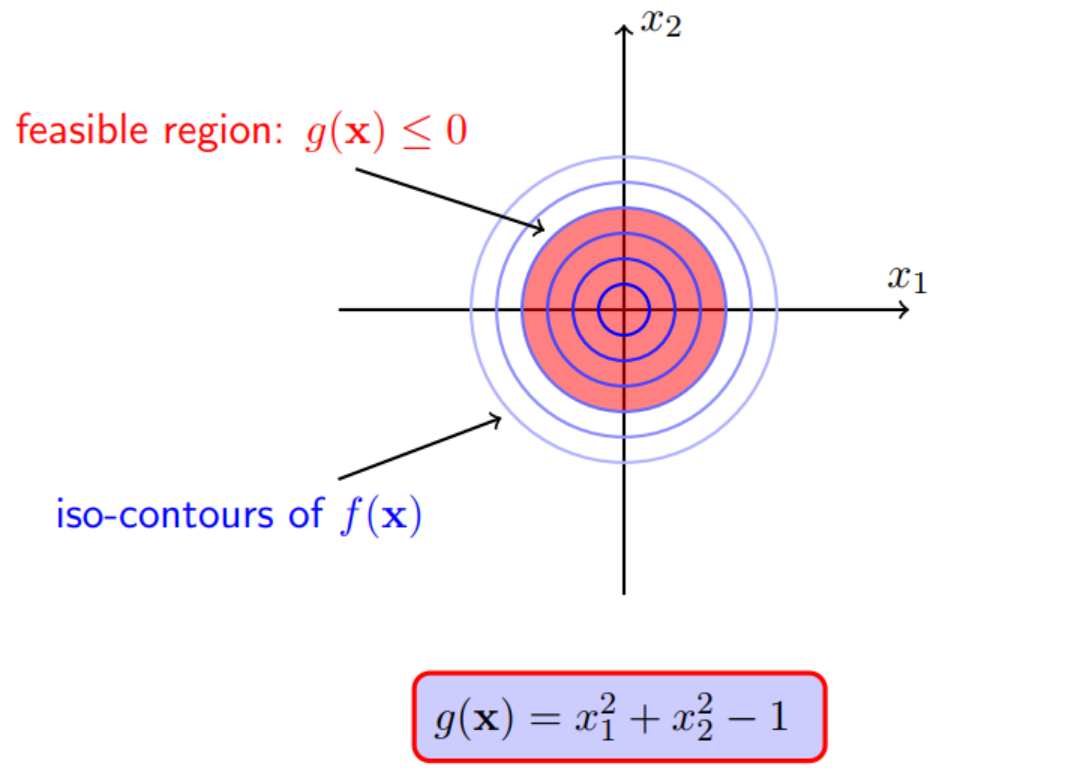
考虑目标函数$f(x)=(x_1−1.1)2+(x_2+1.1)2$ ,不等值约束$g(x)=x_12+x_22−1$,显然f(x)的极小值为原点(1.1, -1.1),落在可行域外。可行域以原点为圆心,半径为1。
这种情况约束起作用,要考虑求解f(x)在可行域内的极小值点。
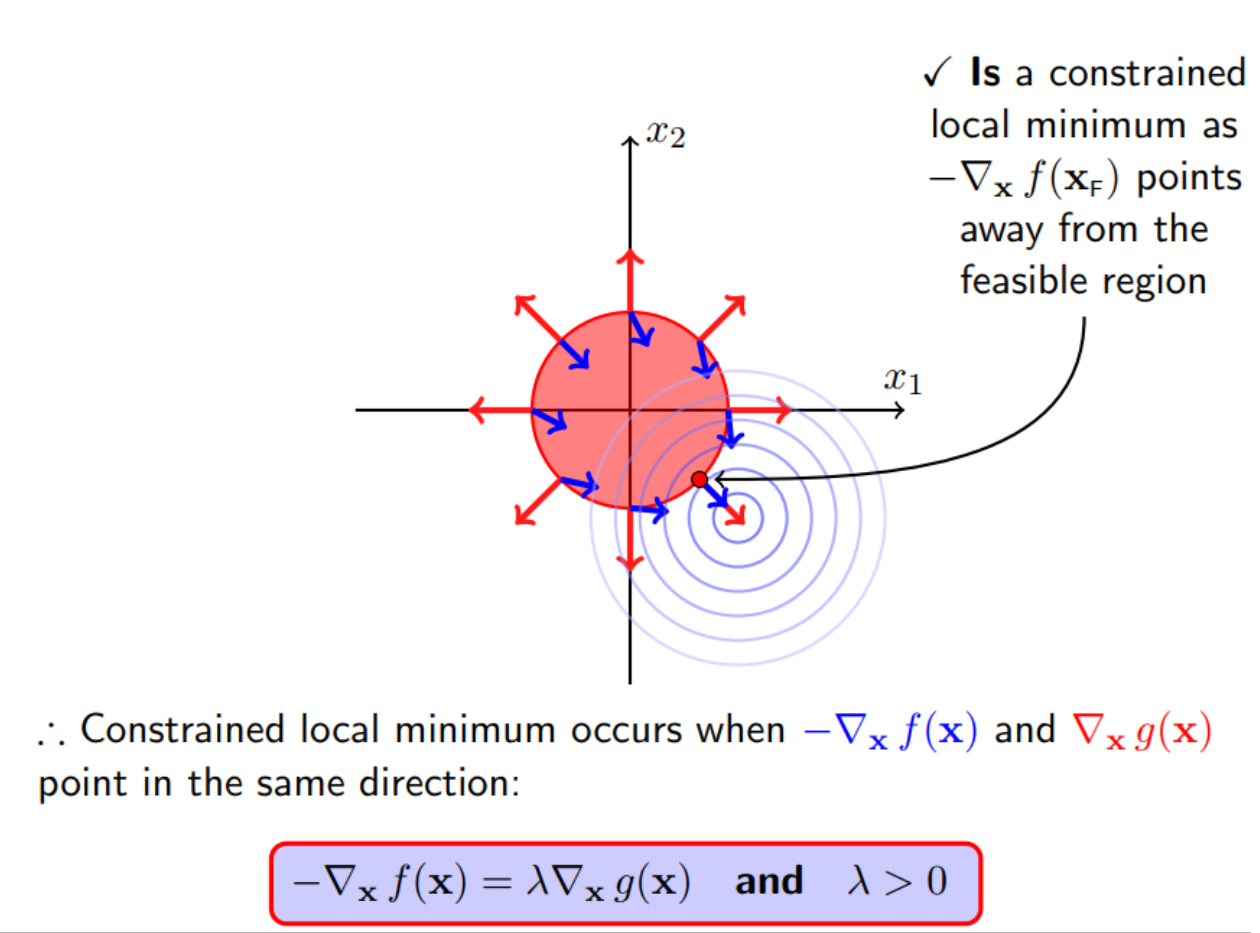
对于f(x)而言要沿着f(x)的负梯度方向走,才能走到极小值点,如下图的蓝色箭头。
这个时候g(x)的梯度往区域外发散,如下图红色箭头。
显然,走到极小值点的时候,g(x)的梯度和f(x)的负梯度同向。因为极小值点在边界上,这个时候g(x)等于0。
¶KKT
复习了上述知识,我们再来看一看拉格朗日乘子法里面这个特别出名的KKT条件,先来看看拉格朗日乘子法考虑等式约束和不等式约束后最后的最终形式:
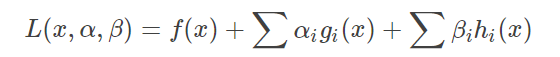
然后再看一眼我们的KKT条件:

前两条非常好理解,即,保证等式约束和导数为零,但第三条是什么意思呢?从字面上意义上看,由于$g(x)$永远是小于等于零的,所以要么某个不等式$g_i(x)=0$,要么其对应的$α_i=0$。
简单说,这个式子exactly描述了我们刚刚说的不等式约束的两种条件:
-
目标函数极值点在约束范围内,则约束无效,直接求解即可。(对应$g_i(x)<0$ ,同时$\alpha_i=0$)
-
目标函数极值点不在约束范围内,则最优解只能在约束边界上。(对应$g_i(x)=0$ ,同时$\alpha_i》0$)
而关于第二点,使用反证法即可(无需分析梯度),因为假设最优解不在边界,而在约束内,那么这个最优解将形成另一个极值点,这与凸的目标函数只有一个极值点矛盾
¶彩蛋
这个时候,再回过头看一眼周志华老师的西瓜书,是不是有点恍然大悟的感觉呢?

