BP算法的两种推导

¶基于交叉熵

¶问题描述

这里首先给出基于交叉熵的损失函数表示方式。

假设有神经网络结构如下：

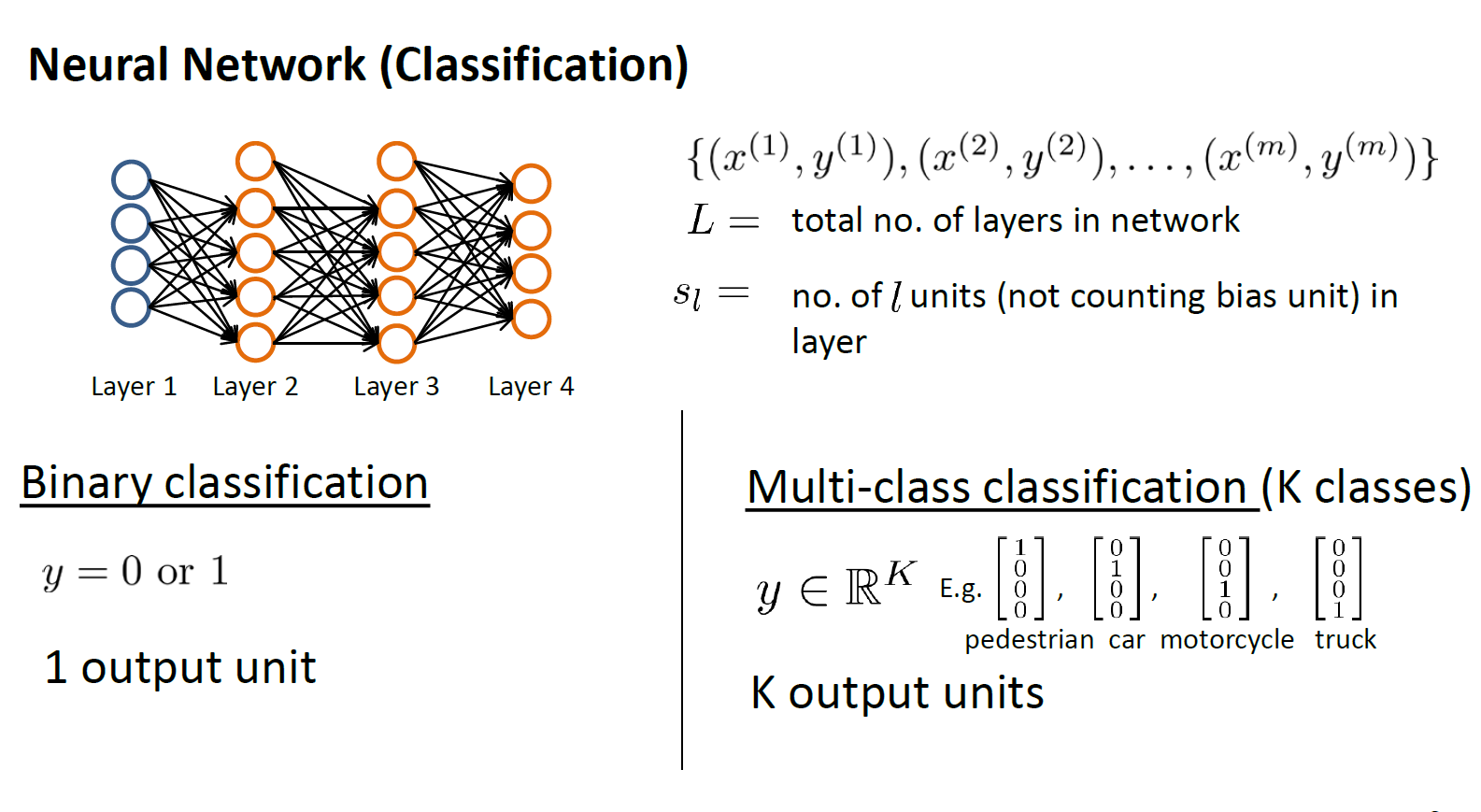
总共有四层，其中第一层是输入层，第四层是输出层，每个隐藏层包含一个偏置项（bias），$L$表示总共的层数，$s_l$表示第$l$层中的神经元个数（不包含偏置项）。

我们可以把这种神经网络想象成K个逻辑斯蒂回归模型的组合，所以很自然的，损失函数需要计算四个输出总共的err，即增加了一层$\sum_{k = 1}^K$用来求和，对应下面的正则化项也很好理解，首先，一共有$L$层说明就有$L-1$个参数集，每个参数集内即可用后两个求和公式进行计算

¶偏导数推导

我们为什么要找到损失函数？因为需要最小化它找到最合适的参数。

我们怎样最小化这个损失函数？最普遍的方式就是梯度下降法（包括随机梯度下降，共轭梯度下降等）。

梯度下降法最关键的步骤是什么？当然是找到梯度。

但是对于神经网络模型来说，参数往往非常多，而且彼此依赖，如何快速计算出损失函数对于每个参数的梯度就是BP算法要解决的问题。

首先，我们再来看刚才的问题：

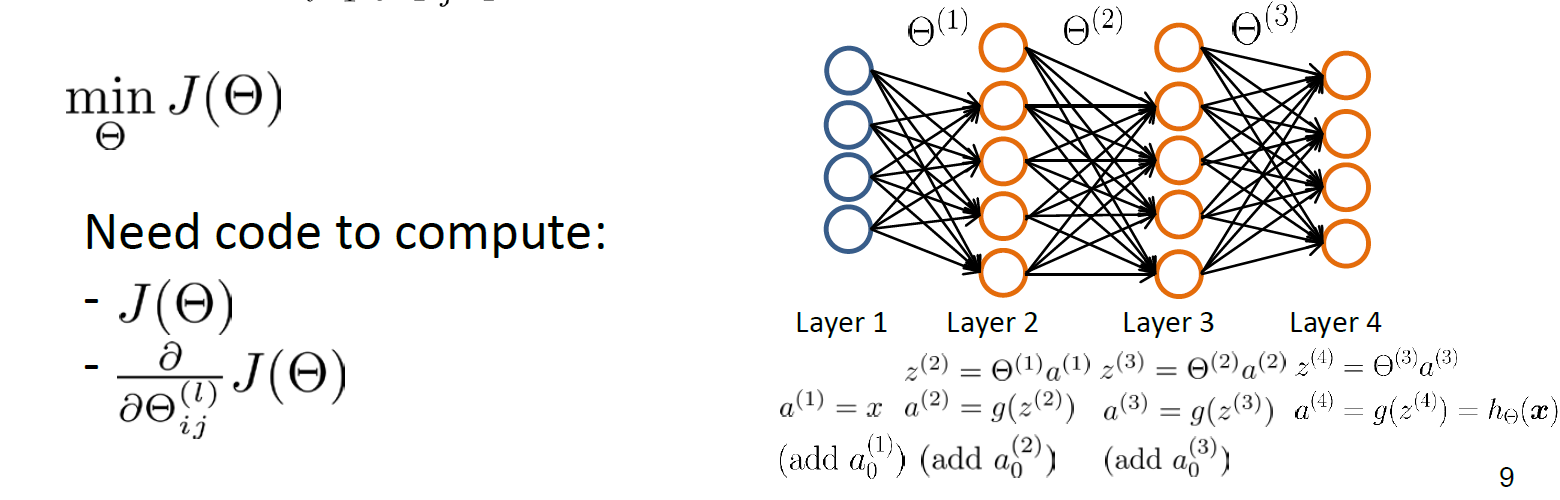
假设 $a$ 代表每一层的输出，$z$ 代表每一层的输入（$z^{(2)} = \Theta^{(1)}a{(1)}$ ），BP算法的厉害之处在于，它先计算出“每个节点的err”，而由链式法则，参数的偏导数即为这个节点的“err”再乘上该节点对该参数的偏导，具体公式如下：

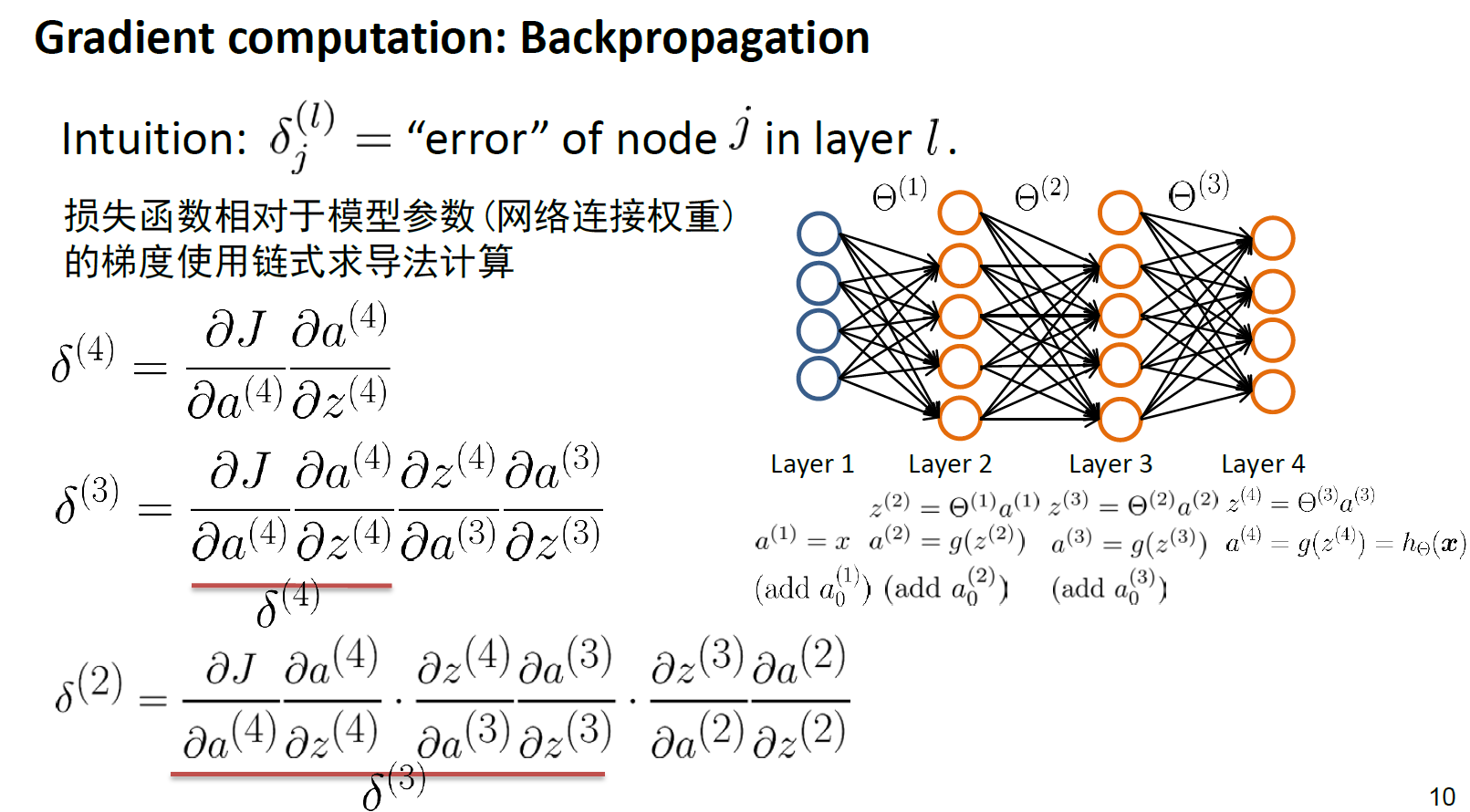
有个这个“节点的err”，再求某个具体参数的偏导，就直接乘上一层偏导就可以了，而这一层偏导就是上一层对应参数的输出 $a$

右上所述，我们就可以对一个样本、一个输出层节点的偏导进行推导：

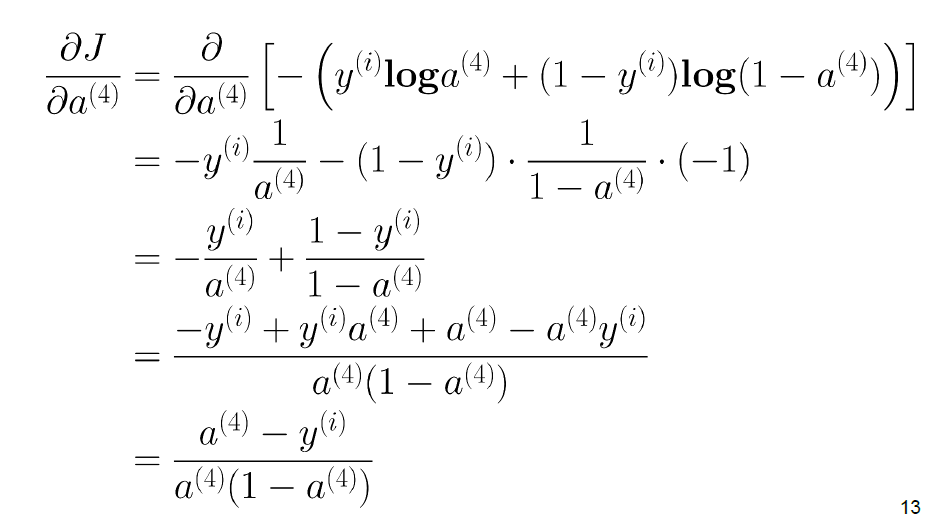
注意这里的$\delta^{(4)}$是一个四行一列的向量，代表的是$J(\Theta)$ 对于四个输出层的四个偏导数，接下俩是第二项，sigmoid的求导

两项相乘，得到的式子非常简洁：

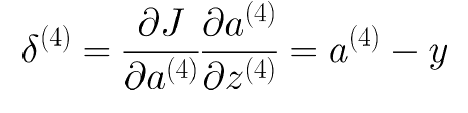
最后，我们对三层节点都求出对应 $\delta$ 如下：

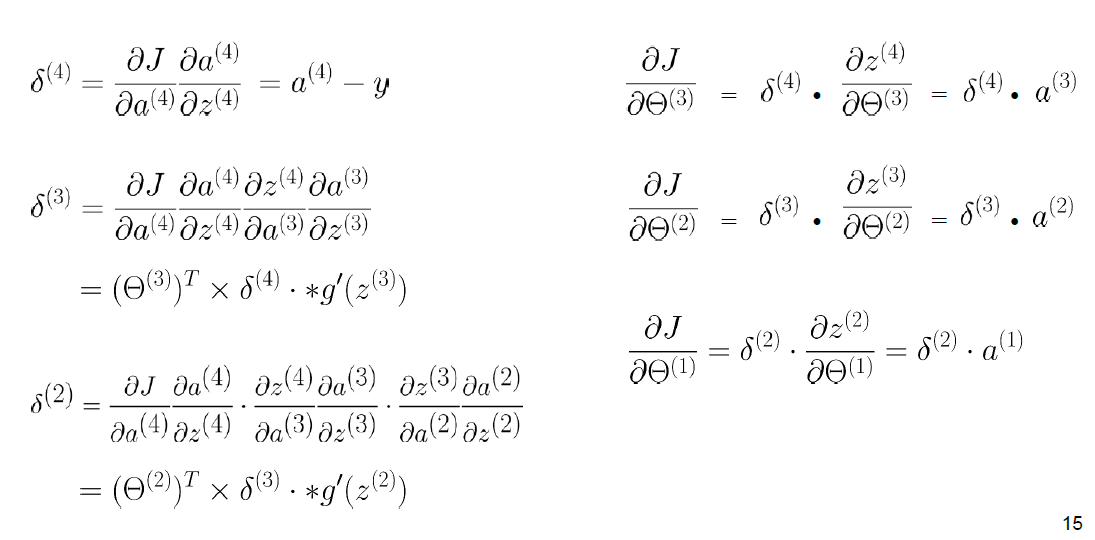
¶最终伪代码

¶基于最小二乘

¶问题描述

这种方法与上述交叉熵不同点就在于损失函数不同，这里使用的是最小二乘法，即最小化下面这个函数

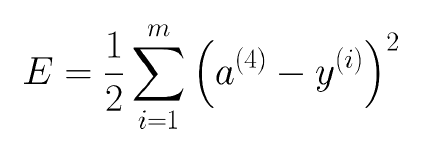
这里对应的$\delta$就是：
$$\delta^{(4)} = \frac{\partial E}{\partial a^{(4)}}\frac{\partial a^{(4)}}{\partial z^{(4)}}$$

$$
=\sum_{i=1}^{m}(a{(4)}-y^{(i)})a{(4)}(1-a^{(4)})
$$

所以有，
$$
\frac{\partial E}{\partial \theta_{ij}^{(3)}} =\delta^{(4)}\frac{\partial z^{(4)}}{\partial \theta_{ij}^{(3)}} = a^{{(3)}\sum_{i=1}}{m}(a^{(4)}-y{(i)})a^{(4)}(1-a{(4)})
$$

¶伪代码

剩下的步骤基本就与上述一致：

这样，我们就完成两种损失函数的BP算法推导，其实核心思想完全一致，就是把对参数的求偏导改为有顺序的，对节点的求偏导，再累积到每个参数上，就可以神奇地一趟完成整个过程。